Niv Haim

I am an AI/ML researcher at Mobileye, working on ML for autonomous vehicles. I did my Ph.D. at Weizmann Institute of Science, advised by Prof. Michal Irani, where I worked on machine learning and computer vision, and more specifically, Generative AI and understanding memorization in neural networks.

I did my Msc. in theoretical astrophysics, advised by Prof. Boaz Katz, and worked with Prof. Yaron Lipman on Geometric Deep Learning. I received my BSc. in computer science and physics from the Technion (Lapidim excellence program alumnus)

Email / Google Scholar / CV / GitHub / LinkedIn / Twitter

Publications

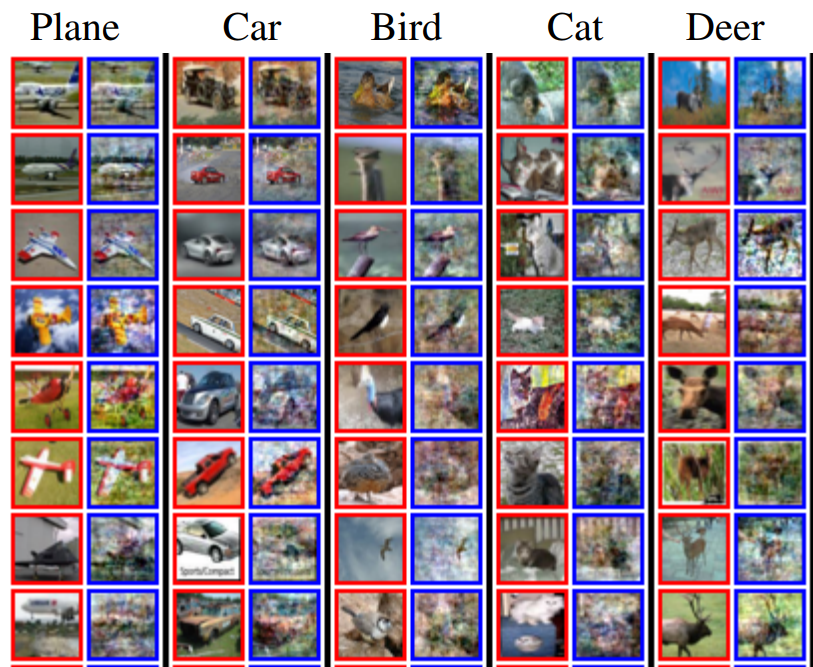
	Deconstructing Data Reconstruction: Multiclass, Weight Decay and General Losses Gon Buzaglo, Niv Haim, Gilad Yehudai, Gal Vardi, Yakir Oz, Yaniv Nikankin, Michal Irani NeurIPS 2023 BibTeX / ArXiv / Code / Video Training set reconstruction from multiclass classifiers and models trained with regression loss with some inriguing observations on the implications of weight decay on reconstructability. (Earlier version appeared in ICLR Workshop on Trustworthy ML, 2023)
	SinFusion: Training Diffusion Models on a Single Image or Video Yaniv Nikankin, Niv Haim, Michal Irani ICML 2023 BibTeX / ArXiv / Code / Project Page Diffusion models can be trained on a single image or video, giving rise to diverse video generation and extrapolation.
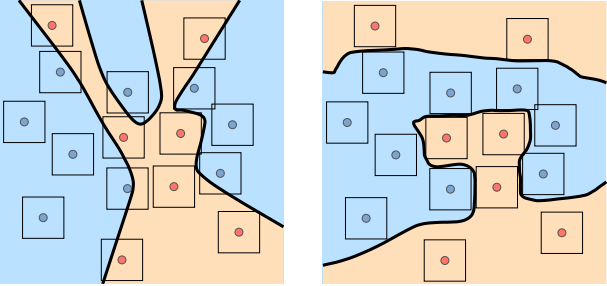
	Reconstructing Training Data from Trained Neural Networks Niv Haim, Gal Vardi, Gilad Yehudai*, Ohad Shamir, Michal Irani NeurIPS 2022 Oral BibTeX / ArXiv / Code / Project Page / Video We show that a large portion of the training data can be reconstructed from the parameters of trained MLP binary classifiers. Our method stems from theoretical results about the implicit bias of neural networks trained with gradient descent
	Diverse Generation from a Single Video Made Possible Niv Haim, Ben Finestein, Niv Granot, Assaf Shocher, Shai Bagon, Tali Dekel, Michal Irani ECCV 2022 BibTeX / ArXiv / Code / Video / Project Page We generate diverse video samples from a single video using patch-based methods. Our results outperform single-video GANs in visual quality and are orders of magnitude faster to generate (Extended abstract appeared at AI For Content Creation Workshop @ CVPR, 2022)
	From Discrete to Continuous Convolution Layers Assaf Shocher, Ben Finestein, Niv Haim, Michal Irani Preprint*, 2020 BibTeX / ArXiv Learning continuous convolution kernels improve translation equivariance and allow test time scales augmentations
	Implicit Geometric Regularization for Learning Shapes Amos Gropp, Lior Yariv, Niv Haim, Matan Atzmon, Yaron Lipman ICML 2020 BibTeX / ArXiv / Code / Video Using an "Eikonal regularization" term with implicit neural representation works surprisingly well for modelling complex surfaces
	Controlling Neural Level Sets Matan Atzmon, Niv Haim, Lior Yariv, Ofer Israelov, Haggai Maron, Yaron Lipman NeurIPS 2019 BibTeX / ArXiv / Code / Poster Making input points differentiable (w.r.t model parameters), and using it for shape modelling, improved robustness to adversrial examples and more
	Surface Networks via General Covers Niv Haim, Nimrod Segol, Heli Ben-Hamu, Haggai Maron, Yaron Lipman ICCV 2019 BibTeX / ArXiv / Code Transforming 3D shapes to image representation so we can feed them to off-the-shelf CNNs and do classification, human-parts segmentation and more
	Extreme close approaches in hierarchical triple systems with comparable masses Niv Haim, Boaz Katz MNRAS 2018 BibTeX / ArXiv / Code Ever wondered if your hierarchical three-body system will eventually collide? find out by plugging your initial conditions into our analytical prediction formula (that works with high probability)

Recorded Talks

Reconstructing Training Data from Trained Classifiers @ Microsoft Data Science Bond

Introduction to Adversarial Examples @ DL4CV2021

Teaching

Weizmann Institute
of Science

Blog Post: How to Give a Good Student Seminar Presentation

Deep Learning for Computer Vision [Winter 2021, Winter 2022]
Advanced Topics in Computer Vision and Deep Learning [Spring 2020, Spring 2021, Spring 2022, Spring 2023]
Deep Neural Networks - a Hands-On Challenge [Spring 2017]

Miscellaneous

I play the violin [YouTube]

I sometimes write about my travels [blog]

This website is based on Jon Barron's homepage template